二叉搜索树提供了平均效率为O(logN)级别的查找、删除、插入操作,但在极端情况下可能导致二叉树退化为单链表。平衡二叉树作为二叉搜索树的一种,通过平衡约束保证左右子树高度相近,能够保证更稳定的性能。本文就从原理出发,最终实现一个操作完备的平衡二叉树。
二叉搜索树BST
维基百科的定义:
In computer science, a binary search tree (BST), also called an ordered or sorted binary tree, is a rooted binary tree data structure whose internal nodes each store a key greater than all the keys in the node’s left subtree and less than those in its right subtree.
二叉搜索树又称为排序二叉树,它满足以下定义:对于BST上的任意一个子树,子树根节点R的左子树上每个节点的key小于根节点R,右子树上每个节点的key大于根节点R。
BST案例如下:
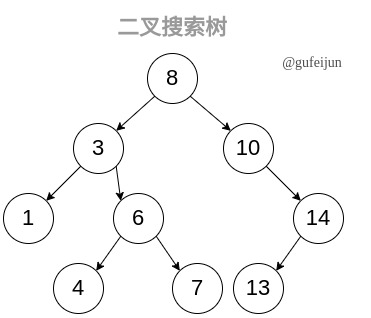
对于查找、删除、插入操作,操作过程中节点之间比较的次数,取决于待操作节点在 BST中的深度。如欲查找节点7,则根据左小右大的原则,查找的路径为8->3->6->7,总共比较4次,即节点7所在的深度。
对于具有n个节点的二叉树,其高度的最大最小满足以下情况:
- 当BST为满二叉树时,高度h最小。h与logN成线性关系。
- 当BST为单支树时,高度h最大。h等于n,此时二叉树退化为单链表。
对于二叉树的操作效率完全取决于树的高度,所以对于一个无其他条件约束的BST,在某些极端条件下,如依次插入有序的数组元素,则会让BST变成单支树,从而使操作效率急剧下降。例依次插入4、5、6、7、8:
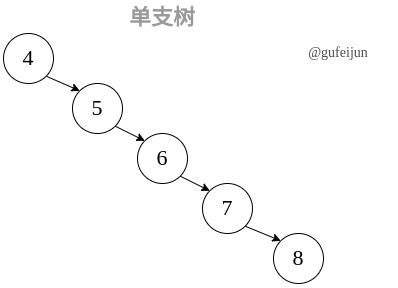
若查找节点9,则需要遍历所有节点,因此BST最坏情况下对其操作的时间复杂度为O(N)。我们需要对BST进行优化。
平衡二叉树AVL
单支树就是因为树高度过高,从而引发了效率低的问题,所以优化的方向就很清晰了。
我们只需要在对BST操作的过程中,让我们的树保证一定的平衡条件,即左右子树高度之间存在一定约束,让节点以比较平均的方式分散到左右子树中,就可以让BST的高度尽量的小。
这样的树叫做自平衡的二叉搜索树(self-balancing binary search tree),其中AVL树就是其中一种,wiki百科定义:
In an AVL tree, the heights of the two child subtrees of any node differ by at most one; if at any time they differ by more than one, rebalancing is done to restore this property.
AVL树在满足BST的基础上,增加了一个平衡条件:任意一个节点的平衡因子(右子树与左子树的高度之差)绝对值小于等于1。通过这种方式,就能有效保证不会出现过长单支树的情况。一旦在对AVL操作的过程中,出现了非平衡的情况,我们需要对树进行调整如旋转,使树重新满足平衡条件。
AVL树案例如下:
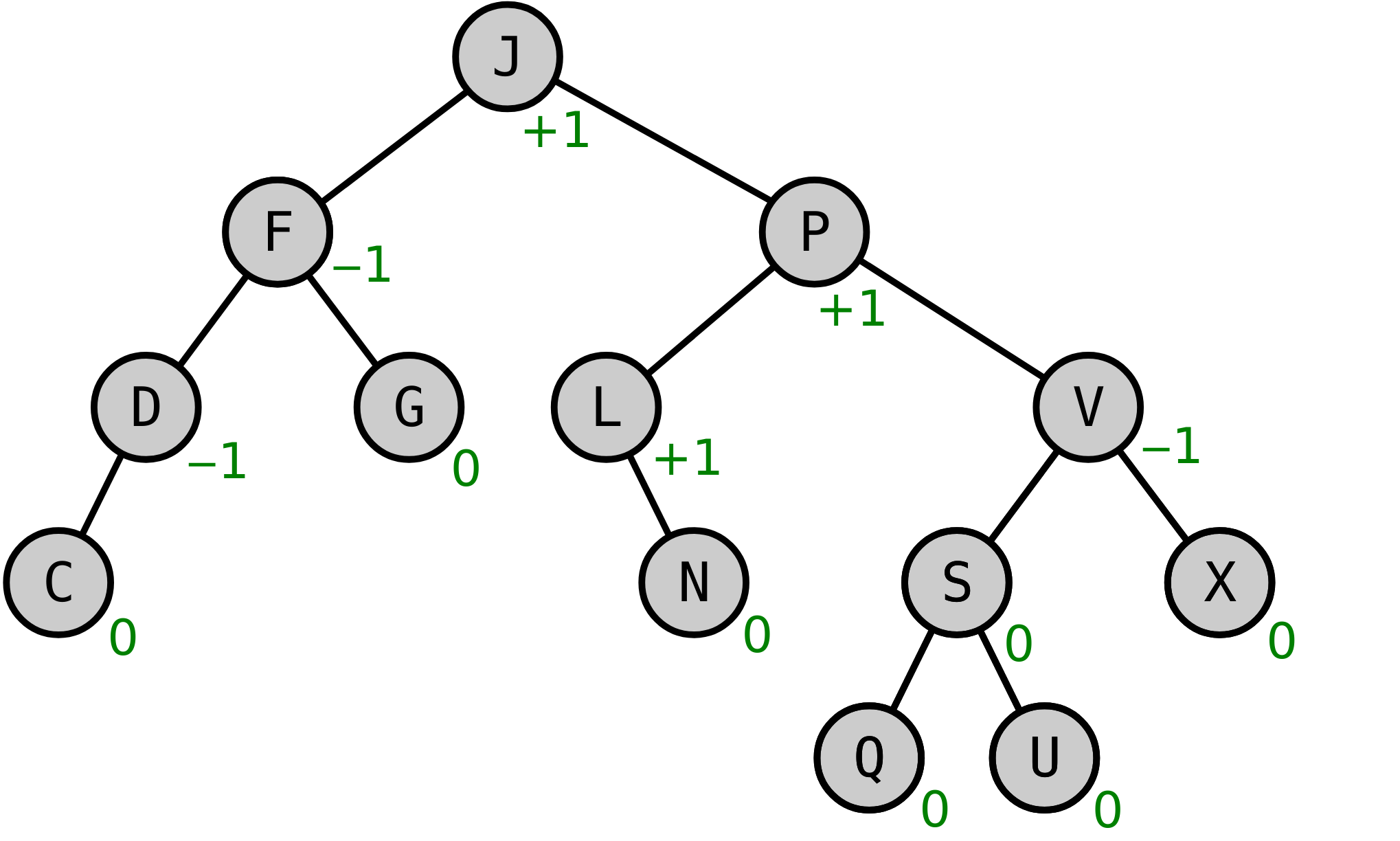
查找
查找过程不会涉及节点数目的变化,因此AVL的查找和BST查找过程相同。从根节点开始不断向下查找,与待查找节点S的key比较,分三种情况:
- 如果当前节点的key与S相同,则找到目标节点,返回该节点即可。
- 如果当前节点的key>S,S只可能出现在左子树,则将当前节点的左孩子与S比较。
- 如果当前节点的key<S,S只可能出现在右子树,则将当前节点的右孩子与S比较。
查询过程使用递归即可,如果迭代到空叶子节点也未找到目标key,则说明avl树并未存储该key,伪代码如下:
1
2
3
4
5
6
7
8
|
node* search(node* root, int key) {
if (root == NULL || root.key == key)
return root;
if (root->key > key)
return search(root->lchild, key);
else
return search(root->rchild, key);
}
|
插入
插入操作导致了节点数目的改变,因此可能导致出现不平衡的情况,对于各种不平衡的情况,需要使用不同的方式进行调整。我们将不平衡的情况分为4种:
LL型:
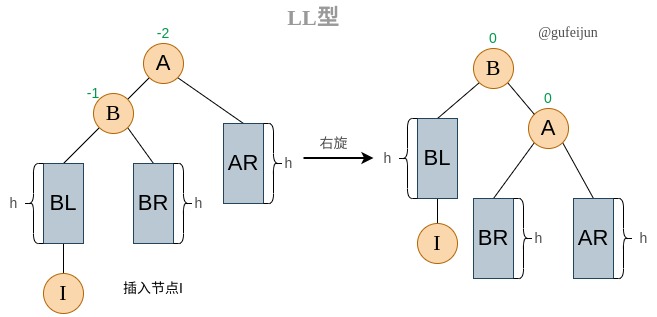
A的平衡因子为-2,A不满足平衡条件。所谓LL型指在非平衡节点A的左孩子的左子树上插入节点导致的不平衡。
对于LL型,我们以B节点作为旋转支点对A进行右旋,即让A变为B的右孩子。既然A需要占用B的rchild指针,我们需要为BR安排去处,正好A的lchild指针会在调整后空缺,可以让BR挂载到A的lchild上,分析可知这样调整也满足BR的每个节点的key小于A这个条件。
RR型:
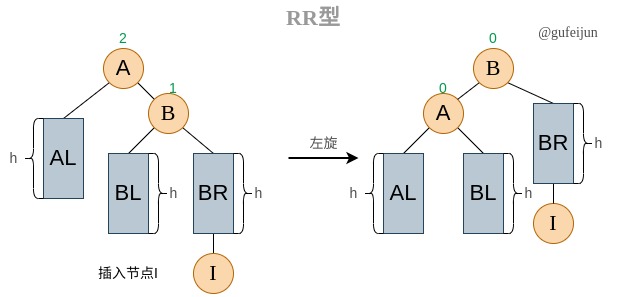
A的平衡因子为2,A不满足平衡条件。所谓RR型指在非平衡节点A的右孩子的右子树上插入节点导致的不平衡。
对于RR型,我们以B节点作为旋转支点对A进行左旋,即让A变为B的左孩子。既然A需要占用B的lchild指针,我们需要为BL安排去处,正好A的rchild指针会在调整后空缺,可以让BL挂载到A的rchild上。
LR型:
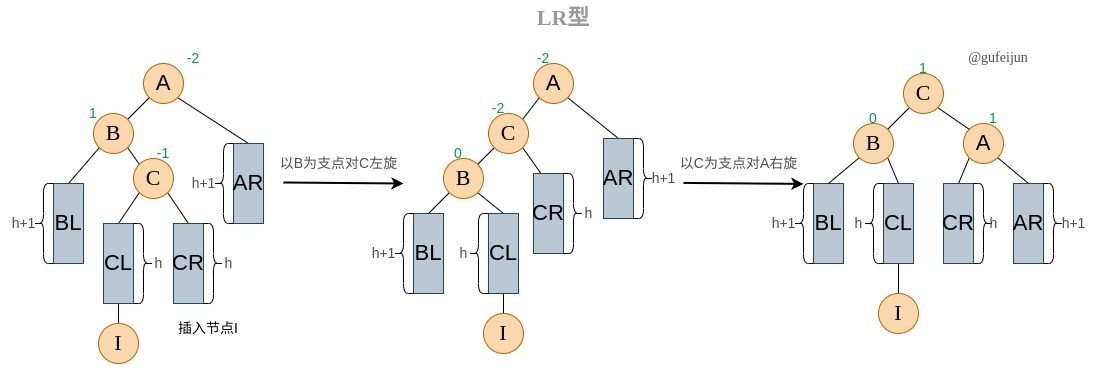
所谓LR型指在非平衡节点A的左孩子的右子树上插入节点导致的不平衡。
对于LR型,旋转是分步进行的。我们先以B为支点对C进行左旋将树其转化为LL型,然后通过右旋将LL型转化为平衡。
RL型:
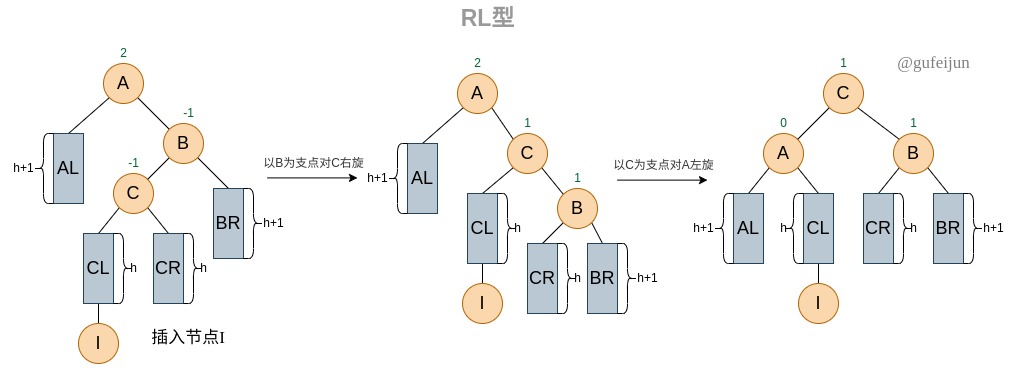
所谓RL型指在非平衡节点A的右孩子的左子树上插入节点导致的不平衡。
对于RL型,和LR型同理。先以B为支点对C进行右旋将树其转化为RR型,然后通过左旋将RR型转化为平衡。
插入步骤:
- 使用递归找到待插入位置并插入。
- 从插入位置不断向上遍历至根节点(需要parent指针),判断这条路径上是否存在不平衡的节点。如果全部平衡,则插入结束,否则找出碰到的第一个不平衡节点,并进入下一步。
- 判断不平衡的类型,并按照对应的方式处理重新调整平衡即可。
删除
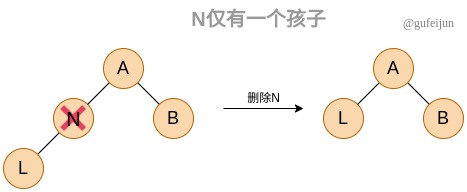
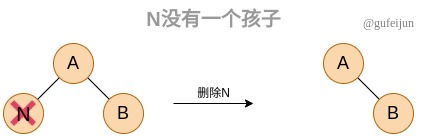
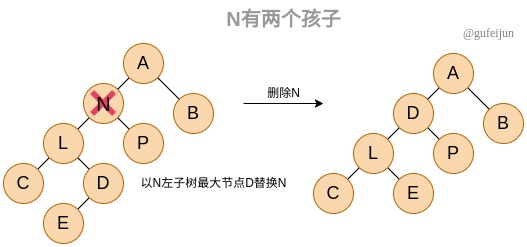
删除某个节点N存在三种情况:
每次删除后,要从删除的节点向根节点不断迭代判断是否平衡,如果不平衡进行调整即可。
如何判断平衡
判断一个子树是否平衡,可有使用递归的方式,伪代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
|
int max(int a, int b) {
return a > b ? a:b;
}
int height(node* root) {
if(root == NULL) return 0;
return 1 + max(height(root->lchild), height(root->rchild));
}
bool IsBalance(node* root) {
if (root == NULL) return true;
int balance_factor = height(root->rchild) - height(root->lchild);
if (balance_factor > 1 || balance_factor < -1)
return false
return IsBalance(root->lchild) && IsBalance(root->rchild);
}
|
但这样效率过于低下,我们采取的解决方案是,让每一个节点保存以该节点为根的子树高度height,这样求某个节点平衡因子,只需要将左右孩子的height相减即可。
显而易见,在插入或者删除的过程中,新插入或者删除的节点可能会影响此节点到根节点这条路径上所有父辈节点的高度,因此我们需要对这些节点的height属性进行更新,更新过程是由下至上的迭代,时间复杂度为O(logN)。
代码实现
本文代码见avl。
数据结构
AVL中每个节点的数据结构如下:
1
2
3
4
5
6
7
8
9
|
//根节点的parent为nil
type node struct {
key int //保存的key
value int //保存的value
height int //以此节点为根的子树高度
parent *node //指向父亲
lchild *node //左孩子
rchild *node //右孩子
}
|
AVL树的数据结构很简单,只需要保存根节点即可:
1
2
3
4
5
6
7
|
type AVL struct {
root *node
}
func NewAVL() *AVL {
return &AVL{}
}
|
需要注意的是,我们让根节点的parent指针为nil,作为由下至上迭代过程的哨兵。
对于node结构绑定了很多辅助方法,比较简单,这里不过多赘述。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
|
// 将n从父亲节点下摘除
func (n *node) detachFromParent() {
if n == nil || n.parent == nil {
return
}
if n.parent.lchild == n {
n.parent.lchild = nil
} else {
n.parent.rchild = nil
}
}
// 获取以@n为根的子树中最大的节点,根据左小右大性质,即为最右节点
func (n *node) maxNode() *node {
for n != nil {
if n.rchild == nil {
return n
}
n = n.rchild
}
return nil
}
// 获取以该节点为根的子树的高度,我们用height属性保存
func (n *node) getHeight() int {
// nil节点的高度为0
if n == nil {
return 0
}
return n.height
}
// 将n的父亲转让给target
func (n *node) shareParent(target *node) {
parent := n.parent
if target != nil {
target.parent = parent
}
//说明n为根节点
if parent == nil {
return
}
if parent.lchild == n {
parent.lchild = target
} else {
parent.rchild = target
}
}
|
查找
查找过程和BST相同,按照左小右大原则即可,不再赘述:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
|
func (avl *AVL) Get(key int) (value int, ok bool) {
target := get(avl.root, key)
if target == nil {
return
}
return target.value, true
}
func get(n *node, key int) (target *node) {
for n != nil {
if n.key == key {
return n
}
if key < n.key {
n = n.lchild
} else {
n = n.rchild
}
}
return nil
}
|
插入
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
|
// 插入操作
func (avl *AVL) Set(key, value int) {
// 如果是第一次插入
if avl.root == nil {
avl.root = &node{
key: key,
value: value,
height: 1,
}
return
}
n := &node{
key: key,
value: value,
height: 1,
}
// 如果已经存在Key了并更新了value,我们不需要执行后续的操作,直接返回
if justUpdate := insert(avl.root, n); justUpdate {
return
}
// 如果树不平衡则进行调整
avl.makeBalance(n)
}
// 插入
func insert(root *node, n *node) (justUpdate bool) {
// 更新操作
if root.key == n.key {
root.value = n.value
return true
} else if root.key < n.key {
if root.rchild == nil {
root.rchild = n
n.parent = root
return
}
return insert(root.rchild, n)
} else {
if root.lchild == nil {
root.lchild = n
n.parent = root
return
}
return insert(root.lchild, n)
}
}
|
如果插入时,AVL已经保存了key,这时就属于更新操作,不会导致树结构的变化,因此不需要担心不平衡的问题。
AVL的insert函数和BST相同,左小右大规则递归即可。重点是makeBalance方法,其任务就是检查插入过程中是否导致不平衡问题,如果有则对AVL进行调整。如下:
1
2
3
4
5
6
7
8
9
10
11
12
|
func (avl *AVL) makeBalance(n *node) {
// 逐次更新节点n的直系父辈节点的高度,时间复杂度O(logN)
unbalanced := adjustHeight(n)
// 如果非平衡节点是根节点,一旦调整树后根节点会改变,我们还需要更改avl的root指针
flag := unbalanced == avl.root
//如果更新高度时,发现了不平衡的节点,则进行调整
if unbalanced != nil {
if subTreeRoot := unbalanced.adjust(); flag {
avl.root = subTreeRoot //更改为调整后子树的根
}
}
}
|
前文提到,插入节点后需要由下至上重新更新该节点的所有父辈高度,使用adjustHeight函数:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
|
// 更新startLeaf到root根节点路径上所有节点的高度。由下至上。
// 更新过程中,如果还找到非平衡节点,则将找到的第一个非平衡节点返回
func adjustHeight(startLeaf *node) (unbalanced *node) {
n := startLeaf
if n == nil {
return nil
}
for {
lh, rh := n.lchild.getHeight(), n.rchild.getHeight()
delta := lh - rh
n.height = max(lh, rh) + 1
// 保存遇到的第一个非平衡节点
if unbalanced == nil && delta > 1 || delta < -1 {
unbalanced = n
}
// 到达根节点
if n.parent == nil {
return
}
// 由下至上
n = n.parent
}
}
|
adjustHeight函数还会顺便检查该条路径上是否存在非平衡节点,如果存在则将其返回,否则返回nil。
接着makeBlance方法中会对非平衡节点unbalanced调用adjust方法进行调整,从而重新达到平衡:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
|
// 对不平衡子树进行调整
// 返回调整后平衡子树的根节点
func (n *node) adjust() *node {
// 判断是什么不平衡类型
lh, rh := n.lchild.getHeight(), n.rchild.getHeight()
if lh < rh {
rlh, rrh := n.rchild.lchild.getHeight(), n.rchild.rchild.getHeight()
// RR类型
if rlh < rrh {
n.adjustRR()
} else { // RL类型
n.adjustRL()
}
} else {
llh, lrh := n.lchild.lchild.getHeight(), n.lchild.rchild.getHeight()
// LL类型
if llh > lrh {
n.adjustLL()
} else { // LR类型
n.adjustLR()
}
}
// 这时n节点的双亲节点就是平衡后子树的根节点
return n.parent
}
|
判断是哪种不平衡类型,从而展开相应的调整即可,LL、LR、RR、RL型调整方法如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
|
// 右旋,将n变为左孩子节点的右孩子
func (n *node) adjustLL() {
lchild := n.lchild
n.shareParent(lchild)
if lchild.rchild != nil {
lchild.rchild.parent = n
}
n.lchild = lchild.rchild
n.parent = lchild
lchild.rchild = n
// 更新高度
n.height = max(n.lchild.getHeight(), n.rchild.getHeight()) + 1
lchild.height = max(lchild.lchild.getHeight(), lchild.rchild.getHeight()) + 1
}
// 左旋,将n变为右孩子节点的左孩子
func (n *node) adjustRR() {
rchild := n.rchild
n.shareParent(rchild)
if rchild.lchild != nil {
rchild.lchild.parent = n
}
n.rchild = rchild.lchild
n.parent = rchild
rchild.lchild = n
// 更新高度
n.height = max(n.lchild.getHeight(), n.rchild.getHeight()) + 1
rchild.height = max(rchild.lchild.getHeight(), rchild.rchild.getHeight()) + 1
}
// 先左旋后右旋
func (n *node) adjustLR() {
n.lchild.adjustRR()
n.adjustLL()
}
// 先右旋后左旋
func (n *node) adjustRL() {
n.rchild.adjustLL()
n.adjustRR()
}
|
LR和RL型是分两步进行的,可以对比着上述的图例进行模拟。
删除
上一节中已经阐述了步骤,代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
|
/* 删除节点N
1、如果N仅有一个孩子,将孩子替代N的位置
2、如果N有两个孩子,将左子树最大值或者右子树最小值替换N,这样也可以满足左小右大的条件
3、如果N没孩子,则直接删除N即可
删除后,需要判断是否满足平衡
*/
func (avl *AVL) Del(key int) {
target := get(avl.root, key)
if target == nil {
return
}
//需要调整高度的节点
var needAdjustHeight *node
if target.rchild != nil && target.lchild != nil { //有两个孩子
// 找到左子树的最大节点即最右节点
lTreeMaxNode := target.lchild.maxNode()
needAdjustHeight = lTreeMaxNode.parent
// 最右节点可能含有左孩子,使其取代父亲的位置
lTreeMaxNode.shareParent(lTreeMaxNode.lchild)
// 交换节点除了可以移动指针外,也可以直接拷贝KV对
target.key = lTreeMaxNode.key
target.value = lTreeMaxNode.value
} else {
// 删除根节点,需要修改avl.root指针,单独讨论
if target == avl.root {
if target.lchild == nil {
avl.root = avl.root.rchild
} else {
avl.root = avl.root.lchild
}
return
}
needAdjustHeight = target.parent
if target.lchild == nil && target.rchild == nil { //没孩子
target.detachFromParent() //摘除即可
} else if target.lchild != nil { //有左孩子
target.shareParent(target.lchild) //以左孩子替代
} else { //有右孩子
target.shareParent(target.rchild) //以右孩子替代
}
}
// 对路径上所有可能更改高度的节点进行高度更新以及调整
avl.makeBalance(needAdjustHeight)
}
|
需要注意的是,删除的节点有两个孩子时,我们选择的是以左子树的最大节点即最右节点进行替换,最右节点可能包含左孩子,需要负责这个左孩子的去向,不要忘了处理这部分。
测试
为了方便迭代AVL元素,给AVL树绑定ForEach方法:
1
2
3
4
5
6
7
8
9
10
11
12
13
|
func (avl *AVL) ForEach(cb func(key, val int)) {
forEach(avl.root, cb)
}
// 中序遍历能够得到已排序的序列
func forEach(n *node, cb func(key, val int)) {
if n == nil {
return
}
forEach(n.lchild, cb)
cb(n.key, n.value)
forEach(n.rchild, cb)
}
|
中序遍历二叉搜索树能得到一个有序序列。
标准的测试应该手动构建各种情况,但限于篇幅原因,我们采用模拟随机使用场景的方式,所以可能不会覆盖所有情况,无法作为标准。测试如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
|
func main() {
avl := NewAVL()
rand.Seed(time.Now().Unix())
// 测试1000次
for t := 0; t < 1000; t++ {
var eleNum int
for i := 0; i < 10000; i++ {
v := rand.Int() % 10000 //随机方式存入若干个10000以内的数
vv, ok := avl.Get(v)
if ok {
if vv != v {
panic(fmt.Sprintf("should got %d, but got %d\n", v, vv))
}
continue
}
//保存非重复key的数量
eleNum++
avl.Set(v, v)
}
var keys []int
avl.ForEach(func(key, val int) {
keys = append(keys, key)
})
if eleNum != len(keys) {
panic(fmt.Sprintf("should have %d elements, but got %d\n", eleNum, len(keys)))
}
for i := 1; i < len(keys); i++ {
if keys[i-1] > keys[i] {
panic("keys are not sorted")
}
}
// 生成一个0~len(keys)这些数随机排列的数组
randArray := makeShuffedArray(len(keys))
// 以随机顺序删除元素
for i := 0; i < len(keys); i++ {
avl.Del(keys[randArray[i]])
}
hasEle := false
avl.ForEach(func(key, val int) {
hasEle = true
})
if hasEle {
panic("should have no elements")
}
}
fmt.Println("test success!")
}
// 随机洗牌算法
func makeShuffedArray(length int) []int {
arr := make([]int, length)
for i := 0; i < length; i++ {
arr[i] = i
}
for i := length - 1; i > 0; i-- {
v := rand.Int() % i
arr[v], arr[i] = arr[i], arr[v]
}
return arr
}
|