上文讲到了利用哈希结构实现map,除此之外还可以用红黑树实现。相较于hash结构的实现,红黑树实现虽然查找删除的时间复杂度由O(1)退化为O(logN),但却拥有更优的空间效率,同时还提供了对key排序的功能,因此广泛应用于数据库存储领域。
红黑树
维基百科定义:
a red–black tree is a kind of self-balancing binary search tree. Each node stores an extra bit representing “color” (“red” or “black”), used to ensure that the tree remains balanced during insertions and deletions.
红黑树是一种自平衡的二叉搜索树,每个节点分为红色与黑色,通过一定的规则保证插入删除时的平衡。
红黑树的平衡条件相较于AVL更为宽松,AVL树见笔者另一篇文章手撕数据结构——平衡二叉树,预先阅读会帮助这篇文章理解。AVL需要任一节点的左右子树高度相差小于等于1,而红黑树是左右子树高度相差小于一倍,因此红黑树在插入删除时更易保持平衡,所需要调整树的次数更少,从而具有更高的效率。
红黑树除了是二叉搜索树外,还满足以下性质:
- 所有null节点都认为是黑色。
- 一个红节点不能有红色孩子,即红色节点之间不能相邻。
- 红黑树中的节点到其任意叶子节点路径上的黑节点个数相同。
- 新插入的节点都是红色,在平衡过程中可能变色。
性质2和性质3就是红黑树的平衡条件。对于一个节点来说,既然左右子树路径上的黑色节点个数相同,因此决定左右子树高度差的因素就是红节点的个数,最极端的情况就是一条子树没有任何红节点,另一条子树尽可能多的有红节点,即红黑节点交替出现(因为红节点之间不能相邻)。因此左右子树高度差不会超过一倍,能够保证查找删除的时间复杂度为O(logN)。
红黑树难就难在如何在插入删除时,保证上述的条件2和条件3的性质。
红黑树案例如图所示,图来自维基百科:

查找
和二叉搜索树一样,不再赘述,详见手撕数据结构——平衡二叉树。
插入
在红黑树中所有新插入的节点都是红色,null节点都是黑色,如果插入后满足上述的条件2和条件3,则不需要调整;否则我们需要通过旋转或者变色等一定操作使树重新平衡。
这里给出一个节点黑色深度的定义:这个节点到任意一个叶子节点上黑色节点的数量。如上图中节点13到任意一条叶子节点路径如13->17->15->Nil上存在三个黑色节点,因此黑色深度为3。
为了讨论方便,我们在此做出以下规定:插入的节点叫做N,N的父亲节点叫做P,N的叔叔节点即P的兄弟节点叫做U,N的祖父节点叫做G。
插入时所有情况如下:
-
如果N为第一个插入红黑树的,让N为根节点即可。
-
如果P是黑色节点。插入红色节点N不会违反条件2和条件3,因此不需调整。
-
如果P是红色节点且U是红色节点。根据条件2则可推断G是黑色,如图所示:

这时P和N两个红节点相邻,违反条件2。我们第一个能想到的解决方案就是让P变为黑色,这样P的黑色深度+1,我们相应的让U也变黑色,让U的黑色深度也加一,就保证了以G为根的子树的平衡。但这样会导致G的黑色深度+1,所以我们进而让G变为红色-1,这样就不会影响G的黑色深度,从而让G与其兄弟节点保持平衡。
但需要注意的是,因为G变为红色,如果G的父亲X也为红色,则违反了条件2,我们这时需要将G当做新一轮N节点进行递归调整。
-
如果P是红色节点且U是黑色节点(性质3可推导U只能为nil节点),这时就存在四种和AVL中类似的不平衡状态。无法单单通过变色保持平衡,需要通过旋转改变树的结构。读者可自行验证下述旋转过程是否保证红黑树平衡。
-
LL型或者RR型。LL型指N是G的左孩子的左孩子,RR型指N是G的右孩子的右孩子。旋转过程注意旋转点G和支点P之间颜色的交换即可。

-
LR型。分两步进行,先以P为支点对N左旋转化为LL型,然后再以N为支点对G右旋。
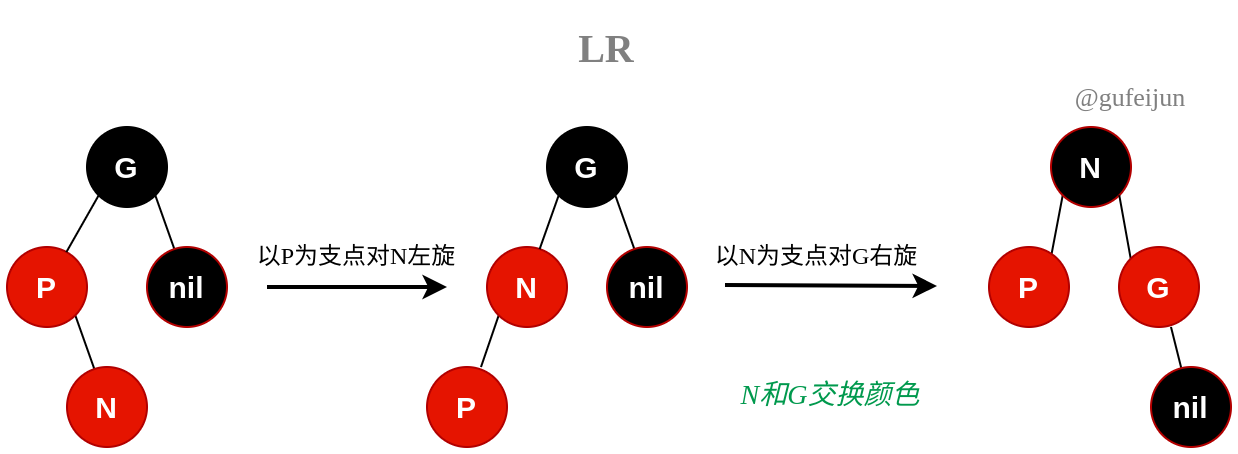
-
RL型。分两步进行,先以P为支点对N右旋转化为RR型,然后再以N为支点对G左旋。
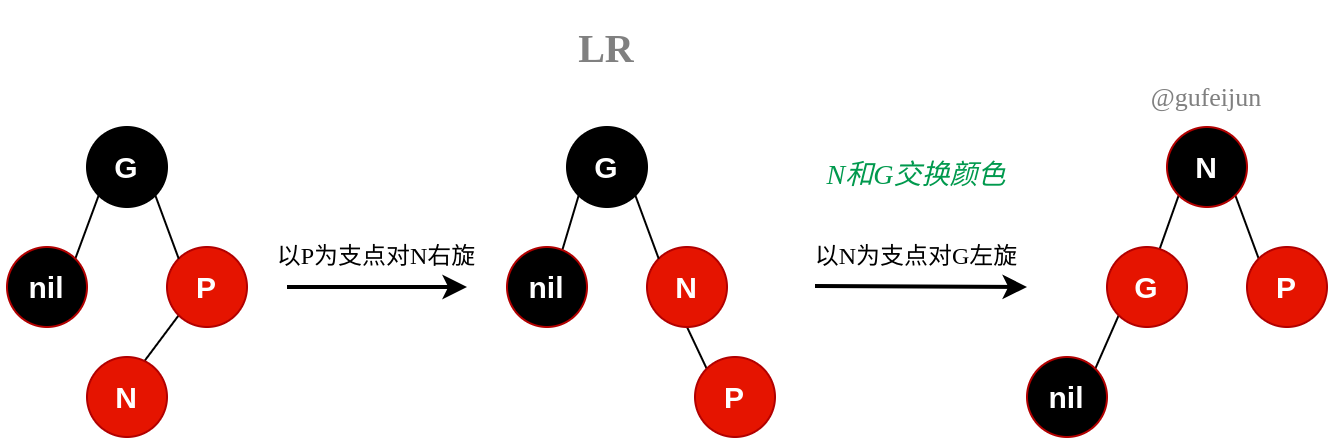
红黑树的插入过程相较于AVL更为简单,AVL需要在插入过程中更新节点高度,而红黑树只需更新节点颜色即可。
删除
删除相较于插入会复杂许多,情况最多,我们使用穷举的方式推导整个过程:
根据待删除节点N孩子个数可以分为三种情况:
1、N有两个孩子。
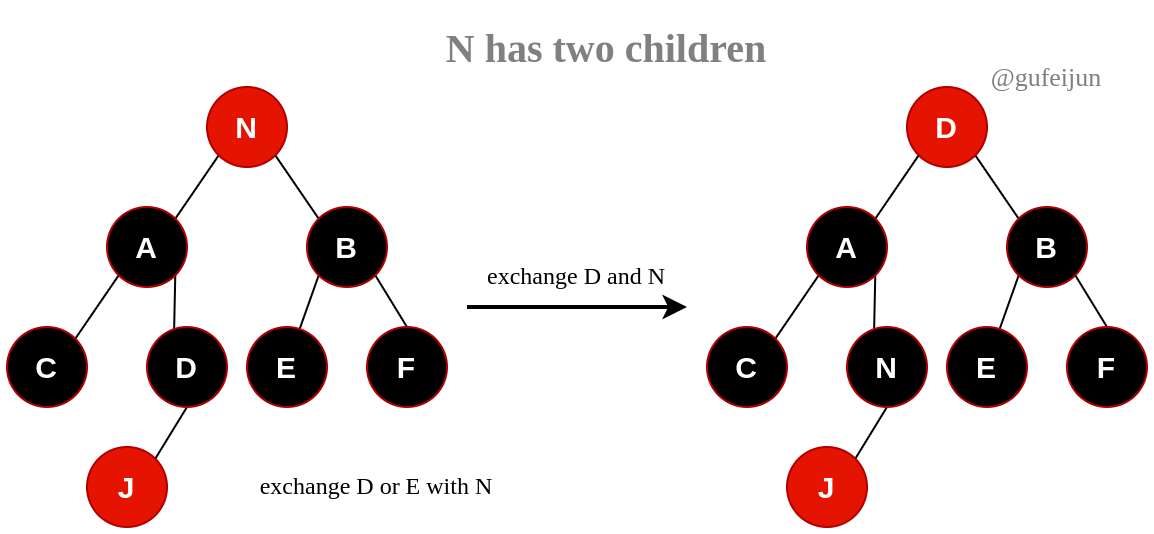
拿左子树最右(即最大)节点如D或者右子树最左(即左小)节点如E与N交换即可。最左和最右节点最多拥有一个孩子,因此这时再去删除N会转化为N有一个孩子或者N无孩子的问题。
2、N有一个孩子。
这时已经能确定N的颜色。因为如果N为红色,则根据条件2孩子必须为黑色,一旦这个唯一孩子为黑色非Nil节点,则左右子树黑色深度相差1,不满足条件3,因此N只能为黑色,孩子只能为红色。如图所示:

调整极为简单,我们只需要将N删除,让孩子替代N的位置,再将孩子变为黑色即可。
3、N没有孩子
这是最复杂的情况,调整的过程涉及父亲P、兄弟S、两个侄子节点C与D。C是空间上与自己最近的侄子(见下图,即N和C要么都是父亲的左孩子,要么都是右孩子),D是另外一个侄子节点。为了描述方便,我们还做出如下规定:
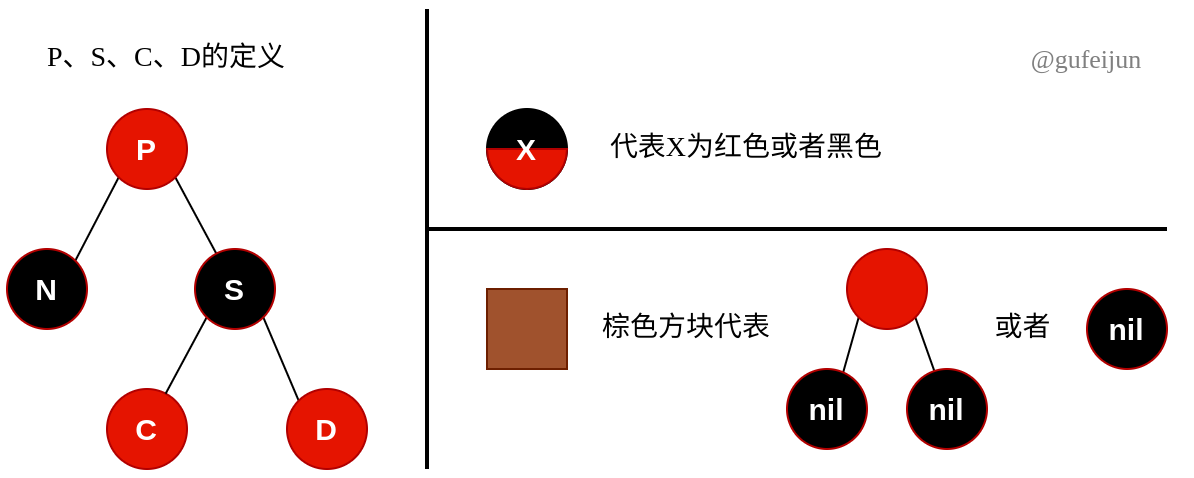
棕色方块代表黑色深度为1的子树。我们再对N为红还是黑进行讨论:
如果N红色,则可以直接删除N,不会违反条件2和3。
下面只需要讨论N为黑色的情况:
①当P为红色时:
那么S则只能为黑色,C和D要么为nil要么为红色,那么会有四种组合:
-
C1:C和D都为黑色。P与S交换颜色即可让P左右子树保证了平衡,同时保证了P的黑色深度不变。
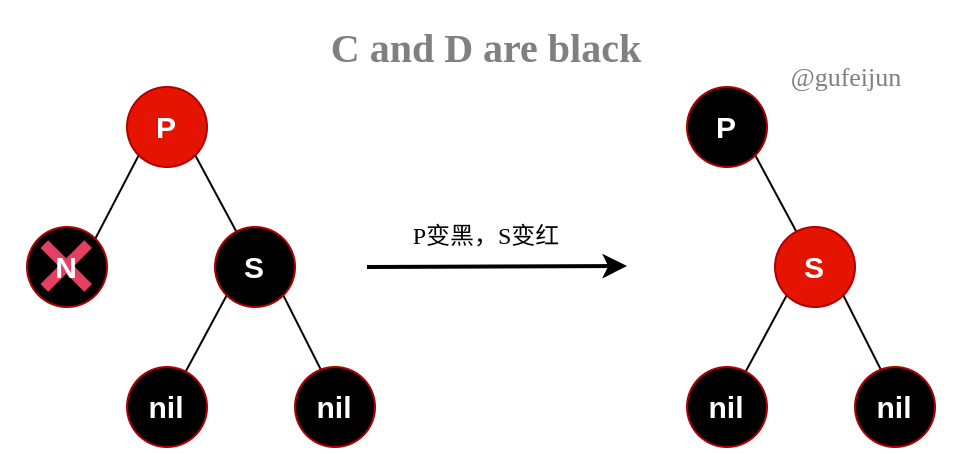
-
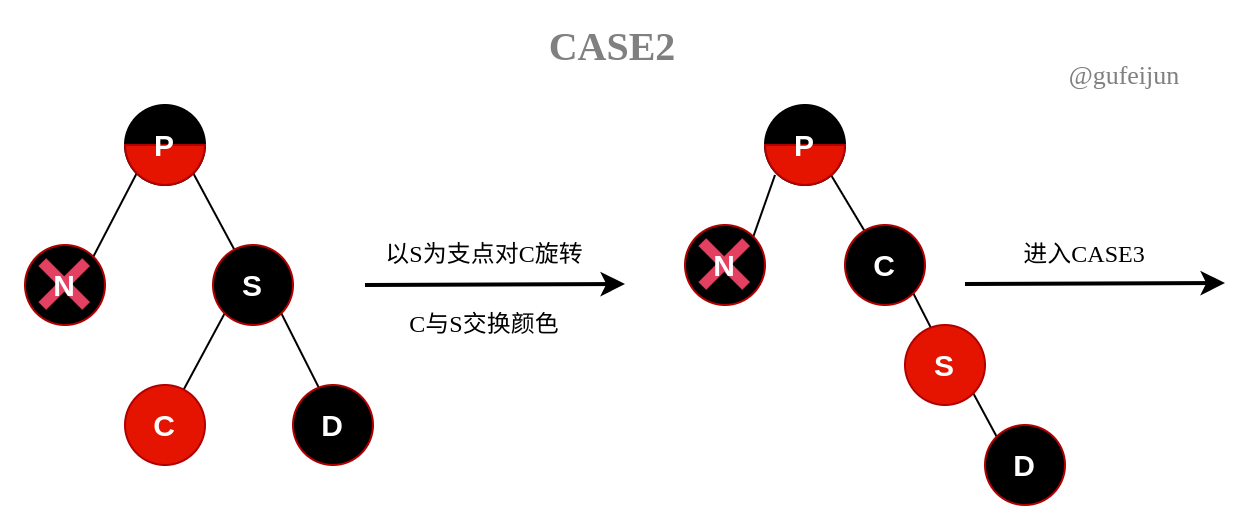
C2:C为红,D为黑色。分两步进行,先以S为支点对C旋转,变成情况C3。

-
C3:D为红色,C为黑或者红。以S为支点对P左旋,S和P交换颜色,D变为黑色即可。
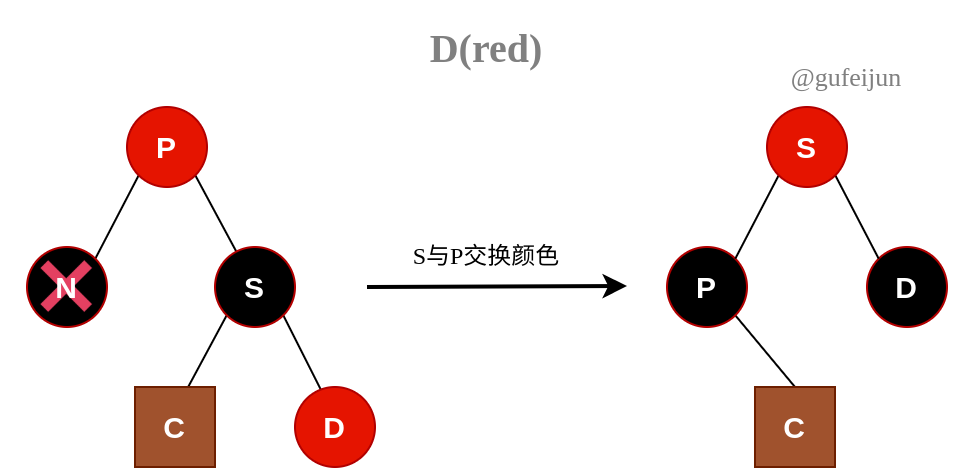
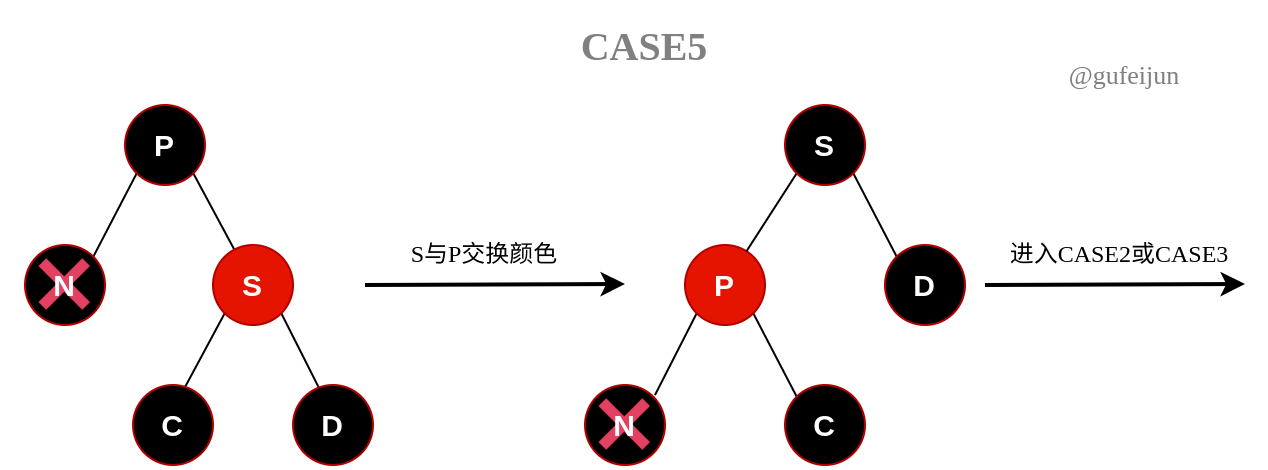
②当P为黑色时:
-
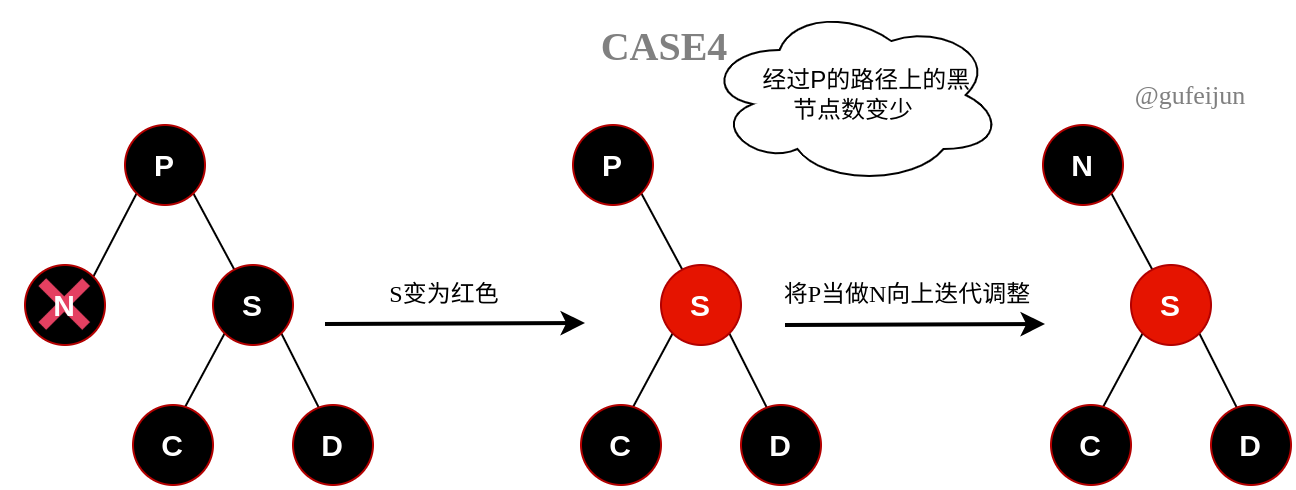
C4:S为红色,则C和D必须为非nil的黑节点。分两步调整,先以S为支点对P旋转,然后再进入C2或者C3状态。
_S(red).png)
-
C5:S为黑色,且C和D都是nil。
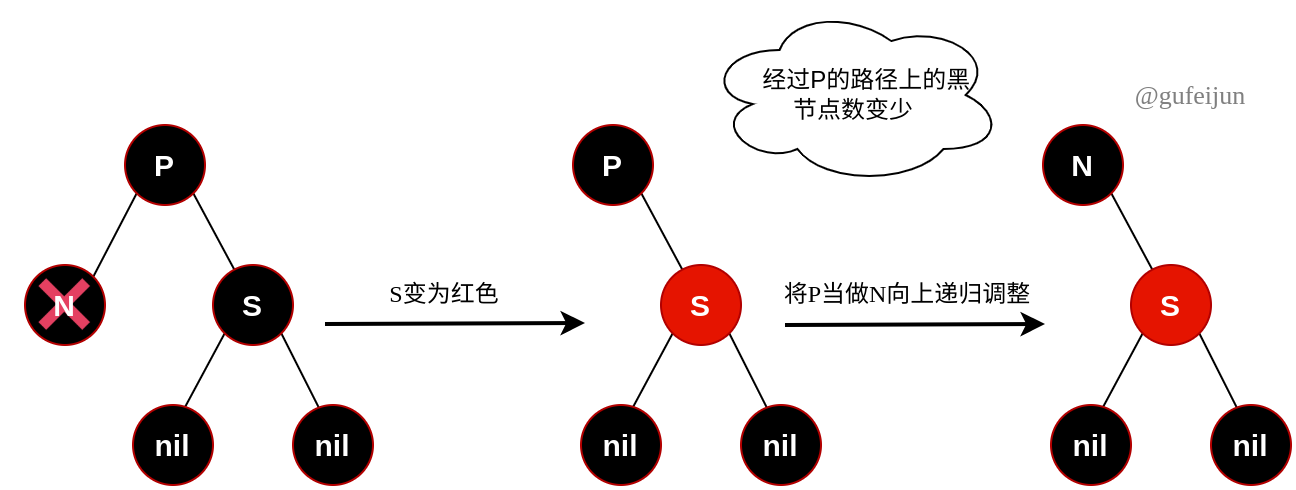
和C1类似,让S变为红色后,P的左右子树能够保证平衡,但P的黑色深度-1,导致P的父亲不满足平衡条件。因此我们需要将P当做N(不过不再需要删除N节点),不断向上迭代调整,直至平衡。
-
C6:S为黑色,C为红色,D为黑色。分两步进行,先旋转后,再进入C7状态。
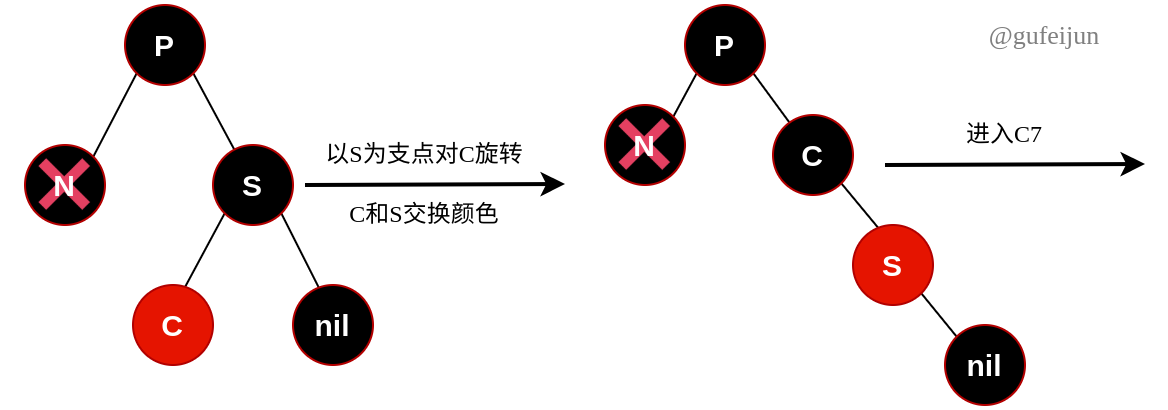
-
C7:S为黑色。D为红色,C为黑色或者红色。

上述就一步步推到了所有情况,有些情况操作相同,可以进行合并,最终只有5种情况:
删除时根据不同情况进行处理即可。
本文是通过穷举方式推导出所有情景后,再进行情况的归并,因此相较于其他文章直接给出结论以及调整步骤的方式,更容易让人接受和理解,不会产生见木不见林的感觉,跟着笔者思路就不需要过多的死记硬背。
代码实现
有了理论知识储备,代码实现是很轻松的,相信读者已经磨刀霍霍准备大展拳脚了,实话实说,这确实是令人挺愉悦的过程,本文代码见rbtree。
数据结构
节点的数据结构如下,很常规:
1
2
3
4
5
6
7
8
9
10
11
12
13
|
type node struct {
color int // 颜色
key int // 保存的key
value interface{} // 保存的value
lchild *node // 左孩子
rchild *node // 右孩子
parent *node // 父亲指针,方便回溯
}
const (
RED = iota
BLACK
)
|
红黑树的数据结构只需要保存根节点即可:
1
2
3
4
5
6
7
|
type RBTree struct {
root *node // 红黑树的根
}
func NewRBTree() *RBTree {
return &RBTree{}
}
|
我们为node结构绑定一些很简单的辅助方法:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
|
// 判断节点颜色
func (n *node) isBlack() bool {
return n == nil || n.color == BLACK
}
// 获取兄弟节点
func (n *node) getSibling() *node {
if n.parent == nil {
return nil
}
if n.parent.lchild == n {
return n.parent.rchild
}
return n.parent.lchild
}
// 返回两个侄子节点,离自己最近的第一个返回
func (n *node) getNephews() (closest *node, another *node) {
p := n.parent
if n == p.lchild {
return p.rchild.lchild, p.rchild.rchild
} else {
return p.lchild.rchild, p.lchild.lchild
}
}
// 获取亲戚,依次返回父亲,兄弟,最近的侄子,另外一个侄子
func (n *node) getRelatives() (parent, sibling, closetNephew, anotherNephew *node) {
parent = n.parent
if parent == nil {
return
}
sibling = n.getSibling()
closetNephew, anotherNephew = n.getNephews()
return
}
// 将n从父亲节点下摘除
func (n *node) detachFromParent() {
if n == nil || n.parent == nil {
return
}
if n.parent.lchild == n {
n.parent.lchild = nil
} else {
n.parent.rchild = nil
}
}
// 获取孩子数量
func (n *node) childCount() (cnt int) {
if n.lchild != nil {
cnt++
}
if n.rchild != nil {
cnt++
}
return
}
// 获取以@n为根的子树中最大的节点,即最右节点
func (n *node) maxNode() *node {
for n != nil {
if n.rchild == nil {
return n
}
n = n.rchild
}
return nil
}
// 让@target指向@n的父亲
func (n *node) shareParent(target *node) {
parent := n.parent
if target != nil {
target.parent = parent
}
//说明n为根节点
if parent == nil {
return
}
if parent.lchild == n {
parent.lchild = target
} else {
parent.rchild = target
}
}
|
辅助方法都比较简单,不再赘述。
查找
按照BST规则查找即可,见Get方法:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
|
func (rbt *RBTree) Get(key int) (interface{}, bool) {
if target := get(rbt.root, key); target != nil {
return target.value, true
}
return nil, false
}
func get(n *node, key int) *node {
for n != nil {
if n.key == key {
return n
}
if key < n.key {
n = n.lchild
} else {
n = n.rchild
}
}
return nil
}
|
插入
见Set方法:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
|
// 插入数据
func (rbt *RBTree) Set(key int, value interface{}) {
// 第一次插入情况
if rbt.root == nil {
rbt.root = &node{
key: key,
value: value,
}
return
}
n := &node{
key: key,
value: value,
color: RED, //新插入的节点为红色
}
// Set数据时可能key已经存在,这时是更新操作,不会出现失衡,直接返回
if justUpdate := insert(rbt.root, n); justUpdate {
return
}
// 检查并保持平衡
rbt.makeBalance(n)
}
|
insert会将节点插入到红黑树中,如果是更新操作不会导致树结构的变化,因此不会出现失衡现象,直接返回即可。
makeBalance方法会检查插入的情况,如果导致了不平衡,我们会对红黑树进行修复。
insert函数和二叉搜索树操作一样,遵循左小右大规则,如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
|
func insert(root *node, n *node) (justUpdate bool) {
if root.key == n.key {
root.value = n.value
return true
}
if root.key > n.key {
if root.lchild == nil {
root.lchild = n
n.parent = root
return
}
return insert(root.lchild, n)
} else {
if root.rchild == nil {
root.rchild = n
n.parent = root
return
}
return insert(root.rchild, n)
}
}
|
makeBalance方法如下,对比前面讨论的情况阅读:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
|
func (rbt *RBTree) makeBalance(n *node) {
// p是父亲节点
p := n.parent
// 父节点为黑色时插入红色节点不会导致失衡
if p == nil || p.color == BLACK {
return
}
// 没有爷爷,即父亲为根节点
if p.parent == nil {
p.color = BLACK // 让根变为黑色即可
return
}
u := p.getSibling() //叔叔
//叔叔是红色时,不需要旋转,只需要变色
if !u.isBlack() {
p.color = BLACK
u.color = BLACK
p.parent.color = RED //祖父
// 因为祖父变为红色,如果祖祖父也是红色的话,需要继续递归调整
rbt.makeBalance(p.parent)
return
}
// 如果祖父p是根节点,则后面的调整可能导致根节点变化,我们这里用flag记录
flag := p.parent.parent == nil
// 父亲为红,叔叔为黑色,需要进行LL、RR、LR或者RL调整
if subTreeRoot := rbt.adjust(n); flag {
rbt.root = subTreeRoot
}
}
|
注释比较全面,这里讲一下前面未讨论到的情况:如果插入节点N的父亲是根节点,直接让根节点变为黑色即可。
在调用adjust方法前,都不需要对树进行结构调整。adjust函数会检测不平衡类型,从而进行相应的处理。
值得注意的是,一旦树进行调整,如果调整过程导致了根节点的变化,我们也要相应的对rbt.root更改。调整过程涉及父亲P、祖父G和叔叔U,即变化都限定在以祖父G为根的子树中,adjust方法会将调整后的该子树的新根返回。adjust如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
|
func (rbt *RBTree) adjust(n *node) *node {
//判断类型
p := n.parent
g := p.parent
if n == p.lchild {
if p == g.lchild { //LL
g.adjustLL()
} else { //RL
g.adjustRL()
}
} else {
if p == g.rchild { //RR
g.adjustRR()
} else { //LR
g.adjustLR()
}
}
return g.parent //读者可自行推导,不论是哪种情况,g.parent都会是新子树的根
}
// 先右旋后左旋
func (n *node) adjustRL() {
n.rchild.adjustLL()
n.adjustRR()
}
// 先左旋后右旋
func (n *node) adjustLR() {
n.lchild.adjustRR()
n.adjustLL()
}
// 左旋
func (n *node) adjustRR() {
rchild := n.rchild
rchild.shareParent(rchild.lchild)
n.shareParent(rchild)
rchild.lchild = n
n.parent = rchild
n.color, rchild.color = rchild.color, n.color
}
// 右旋
func (n *node) adjustLL() {
lchild := n.lchild
lchild.shareParent(lchild.rchild)
n.shareParent(lchild)
lchild.rchild = n
n.parent = lchild
n.color, lchild.color = lchild.color, n.color
}
|
旋转过程和AVL树一样,详见AVL,不过需要额外注意下颜色的变化。旋转时,要将旋转点和支点进行颜色交换。
删除
重难点在于删除,相较于插入,情况更多,好在我们前面用穷举全部列举一遍,对照处理即可。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
|
// 删除
func (rbt *RBTree) Del(key int) {
// 先找到待删除节点
target := get(rbt.root, key)
if target == nil {
return
}
rbt.del(target)
}
func (rbt *RBTree) del(target *node) {
// 获取待删除节点孩子个数
cnt := target.childCount()
switch cnt {
case 0:
// 如果删除节点就是根节点
if target == rbt.root {
rbt.root = nil
return
}
// 如果删除节点是红色节点
if target.color == RED {
target.detachFromParent()
return
}
// 删除黑色叶子节点
rbt.delBlackLeaf(target)
case 1: // 这时target一定是黑色,孩子一定是红色,用孩子替换target即可
var child *node
if target.lchild != nil {
child = target.lchild
target.lchild = nil
} else {
child = target.rchild
target.rchild = nil
}
target.key, target.value = child.key, child.value
case 2:
// 以左子树最右孩子替换,这样就能转化为case 0或者case 1情况。
replace := target.lchild.maxNode()
target.key, target.value = replace.key, replace.value
rbt.del(replace)
}
}
|
有一个孩子的情况很好处理,用孩子替换待删除节点即可。
有两个孩子的情况中,可以用target的左子树最大或者右子树最小节点与target替换,这样就能转化为待删除节点只有一个孩子或者无孩子的情况。
无孩子是最复杂的,见delBlackLeaf,与上文讨论的五种CASE对照阅读:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
|
// 删除无孩子的黑色叶子节点
func (rbt *RBTree) delBlackLeaf(target *node) {
// p父亲,s兄弟,c为离自己最近的侄子,d为另外一个侄子
p, s, c, d := target.getRelatives()
// 删除target
target.detachFromParent()
//CASE4和CASE5需要多次迭代,所以用for循环
for target != rbt.root {
if s.isBlack() && c.isBlack() && d.isBlack() { // CASE1、CASE4
if !p.isBlack() { //CASE1
p.color, s.color = BLACK, RED
break
}
s.color = RED
// CASE4中经过p的路径上黑节点个数变化
// 因此需要以p做新一轮target向上迭代进行调整
target = p
if target == rbt.root {
return
}
p, s, c, d = target.getRelatives()
} else if !c.isBlack() && d.isBlack() { // CASE2
if s == p.rchild {
p.adjustRL()
} else {
p.adjustLR()
}
if p == rbt.root {
rbt.root = c
}
s.color = BLACK
break
} else { // CASE3、CASE5
if s == p.rchild {
p.adjustRR()
} else {
p.adjustLL()
}
if p == rbt.root {
rbt.root = s
}
if !d.isBlack() { //CASE3
d.color = BLACK
break
}
// 对于CASE5,需要再进入CASE2或者CASE3进行新一轮调整
s = c
if s == p.rchild {
c, d = s.lchild, s.rchild
} else {
c, d = s.rchild, s.lchild
}
}
}
}
|
测试
为了方便顺序迭代红黑树元素,绑定ForEach方法:
1
2
3
4
5
6
7
8
9
10
11
12
13
|
func (rbt *RBTree) ForEach(cb func(key int, val interface{})) {
forEach(rbt.root, cb)
}
// 中序遍历能够得到已排序的序列
func forEach(n *node, cb func(key int, val interface{})) {
if n == nil {
return
}
forEach(n.lchild, cb)
cb(n.key, n.value)
forEach(n.rchild, cb)
}
|
标准的测试应该手动构建各种情况,但限于篇幅原因,我们采用模拟随机使用场景的方式,所以可能不会覆盖所有情况,不太规范。大致过程是随机插入一些的数,然后以随机方式对数进行删除,测试如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
|
func main() {
rand.Seed(time.Now().Unix())
for i := 0; i < 10000; i++ { //测试10000次
test()
}
fmt.Println("test success!")
}
func test() {
rbt := NewRBTree()
var eleNum int
for i := 0; i < 1000; i++ {
v := rand.Int() % 1000 //随机方式存入若干个1000以内的数
vv, ok := rbt.Get(v)
if ok {
if vv.(int) != v {
panic(fmt.Sprintf("should got %d, but got %d\n", v, vv))
}
continue
}
//如果没有存储该数据
eleNum++
rbt.Set(v, v) // 存入键值一样
}
var keys []int // keys保存排序后的键
rbt.ForEach(func(key int, val interface{}) {
keys = append(keys, key)
})
if eleNum != len(keys) {
panic(fmt.Sprintf("should have %d elements, but got %d\n", eleNum, len(keys)))
}
// 判断keys是否排序
for i := 1; i < len(keys); i++ {
if keys[i-1] > keys[i] {
panic("keys are not sorted")
}
}
// 生成一个0~len(keys)这些数随机排列的数组
randArray := makeShuffedArray(len(keys))
// 以随机顺序删除元素
for i := 0; i < len(keys); i++ {
// 随机访问keys的数组下标,并对元素删除
rbt.Del(keys[randArray[i]])
}
hasEle := false
rbt.ForEach(func(key int, val interface{}) {
hasEle = true
})
if hasEle {
panic("should have no elements")
}
}
// 洗牌算法
func makeShuffedArray(length int) []int {
arr := make([]int, length)
for i := 0; i < length; i++ {
arr[i] = i
}
for i := length - 1; i > 0; i-- {
v := rand.Int() % i
arr[v], arr[i] = arr[i], arr[v]
}
return arr
}
|
系列目录











_S(red).png)