一个系列彻底搞懂map(一):hash表
map映射结构频繁地运用在日常的开发之中,因此成为了面试中的高频考点,本系列将从map的两种实现(hash以及红黑树)出发,再详解go语言的map,最后讨论如何实现高性能的并发安全map,彻底搞懂map结构的奥秘。
什么是map
维基百科的定义:
In computer science, an associative array, map, symbol table, or dictionary is an abstract data type composed of a collection of (key, value) pairs, such that each possible key appears at most once in the collection.
map又称为关联数组、字典、映射,是一个抽象的数组结构,用于存取1:1映射的键值对。其实数组也是一种映射结构,提供数组索引到值的映射,但数组的索引必须为整数类型,而map却可以让键为任何可比较类型如字符串。
map一般会提供如下操作:增删改查键值对。map大致有两种底层数据结构实现:hash表以及红黑树。根据实现的不同,从而具有不同的特性以及存取效率。
-
hash表也称散列表,实现采用空间换时间的思想,理想情况下能让hash map的平均存取效率达到O(1),最坏情况下退化为O(n),hash表采用哈希函数将键值对打散到不同的桶中,对桶的顺序遍历无法做到对键的排序。
-
红黑树是一种平衡二叉查找树结构,插入时保持左子树每个节点的key小于根节点,右子树每个节点的key大于根节点,这种特性使得红黑树实现的map能够进行排序。为了防止极端情况下可能出现单支树,从而使时间复杂度退化为O(n),对二叉查找树的插入和删除都会使其保持平衡(非严格平衡条件),因此红黑树的性能极为稳定,能够保持在O(logN)。
golang的map、python的dict以及c++的unordered_map采用hash实现,c++的map采用红黑树实现,在java1.8的哈希表的实现中采用的是红黑树与哈希结构混合的方式。
不论是上述哪一种实现,都是面试的高频考点,时常被要求手写。本系列前两章就用这两种方式实现最简单的map结构,让你最快速地把握map的本质。在了解最核心原理后,会详解go语言的原生map结构以及其中的众多优化技巧。除此之外,我们会简单剖析下开源库concurrent-map,分析如何实现一个高性能的并发安全的map。
hash表原理
如果让你实现一个结构,能够提供键值对的增删改查,最容易想到的就是使用链表实现。欲插入键值对,只需要将键值对构成一个节点插入链表;给定Key查找Value,只需要从链表头开始迭代所有节点,比较节点的key即可。
但问题是这样实现查找的效率很低,为O(N)。hash表采取了空间换时间的方式,其核心思想是开辟一个数组空间,数组中每个元素称为桶,我们用这些预先分配的桶存储键值对。
那么问题就是如何组织键值对放入到这些有限桶中。对于hash表来说,都会存在一个哈希函数,输入一个key,通过某种hash(key)函数的计算能够输出一个确切的哈希值,且这个过程是幂等的。给定key就能得到哈希值,进而确定将这个KV(key-value)对存储在哪一个桶中。
举个最简单的例子:我们现在拥有10个桶,现在插入一个key为21的键值对,hash函数为f(key)=key%10,则21得到的hash值为1,我们就将这个键值对存到第2(数组下标从0开始)个桶。当下次再查找21时,我们用同样的哈希函数得到同样的哈希值,立马定位到第2个桶,进而查找即可。这样进行就可以省略掉链表实现中遍历所有节点的过程,将查找效率提升到O(1)。
哈希冲突:桶是预分配且有限的,除此之外不同的key可能通过hash函数得到同样的hash值,如31和21通过上述的hash函数都得到1,两个不同键放入同一桶,这样就会导致冲突,这样哈希值相同的Key称为同义词。

21和31就为同义词,一山不容二虎,那么如何去解决冲突问题呢?①开放地址法。②拉链法。
开放地址法
开发地址法的意思是一个桶并不一定只能存放符合哈希要求的键,如下标为2的桶不一定只能存求余为2的key。
例如,目前要依次插入键21、31、23、41、47。key 21插入到桶1中;在准备插入31时,由于桶1已经被key 21占用,我们可以将31插入到桶1后遇到的第一个空桶即桶2;key 23插入到桶3中;在插入41时,本应存入桶1,但由于桶1、桶2、桶3都被占用,key 41就被迫存入空桶4;key 47存入桶7.
对于查找也同理,给定key 31,我们先查看桶1,判断桶里的key与31是否相同,相同则找到目标值,不同则可能存在同义词,去依次查看桶2、桶3、桶4等后续桶,直至找到空桶或者目标key,找到空桶说明待查找的key并没有存于map中。如图所示:
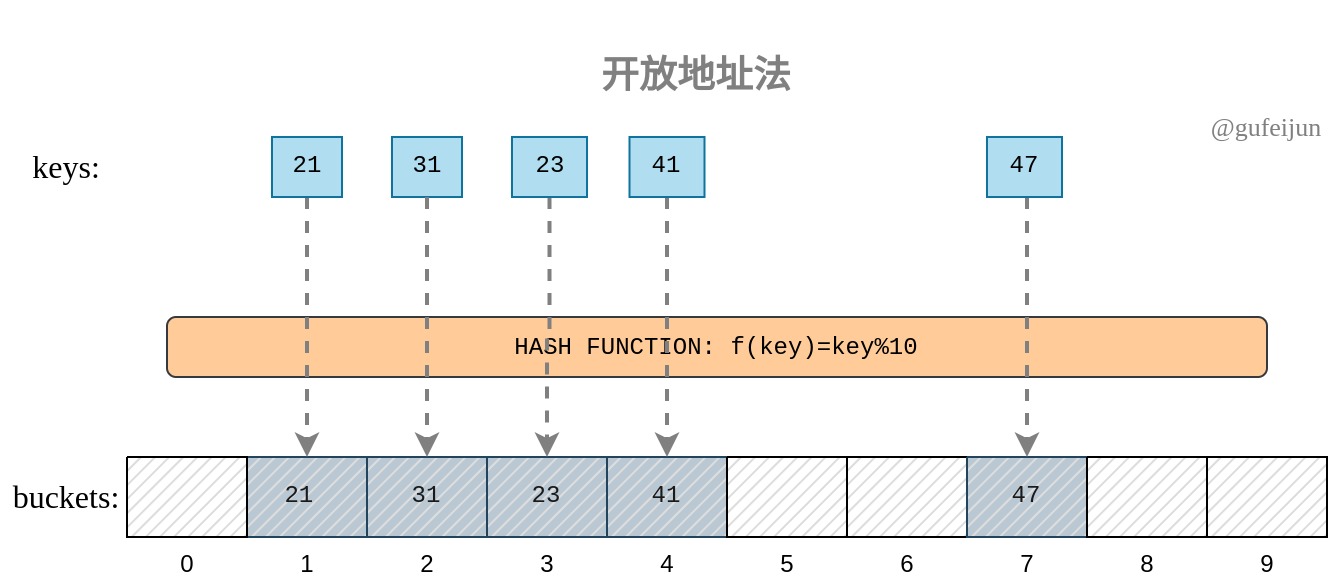
很明显的是,通过这种方式,一旦map的负载因子(键值对个数与桶个数比值)过大,查找需要线性遍历多个桶,性能会退化为O(n),所以这种实现需要更频繁地对桶进行扩容,保持负载因子在低水平。
拉链法
拉链法是大多数编程语言的选择,采用数组以及链表实现。依旧是预先开辟一定容量的桶(数组),不过和开放地址法的区别是,每个桶后面跟上一个链表,所有的同义词通过链表中节点形式串联在一起。如上例中key 31、21和41就可以跟在桶1的链表中,查找时通过hash函数定位桶以区分非同义词,遍历桶的链表每个节点以及比较key来区分同义词。
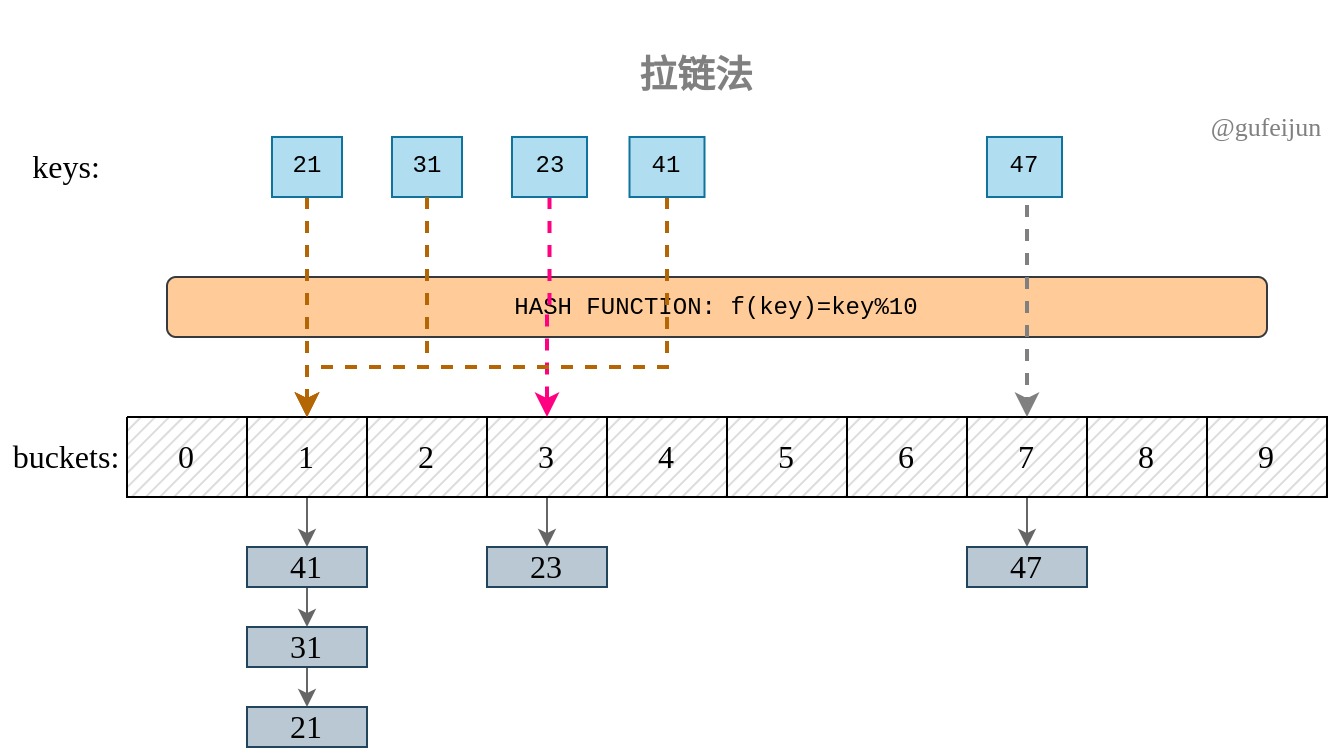
开放地址法存在堆积问题,比如key1可能因为同义词占用了key2的位置,导致key2插入时又不得不占用key3的位置,所以开发地址法对负载因子过于敏感。而拉链法通过链表方式解决冲突问题,非同义词之间不会相互影响。
代码实现
本文代码见hashmap。
为了简便起见,我们map实现中键值都为int类型,因此hash函数直接利用求余函数即可。不同key类型只是对应的hash函数不同而已,不是map的核心思想,我们从简。
开放地址法
开发地址法的实现比较简单,但需要有一点注意,在删除操作中,被删除清空的桶不能直接标记为空桶。如上例中21、31、41为同义词,哈希值都为1,则按照开发地址法的原理,则它们分别存储的桶编号为1、2、3。如果在删除31时将桶2置为空,则查找41时,还没迭代到桶3就止步于空桶2,从而返回错误的结果。
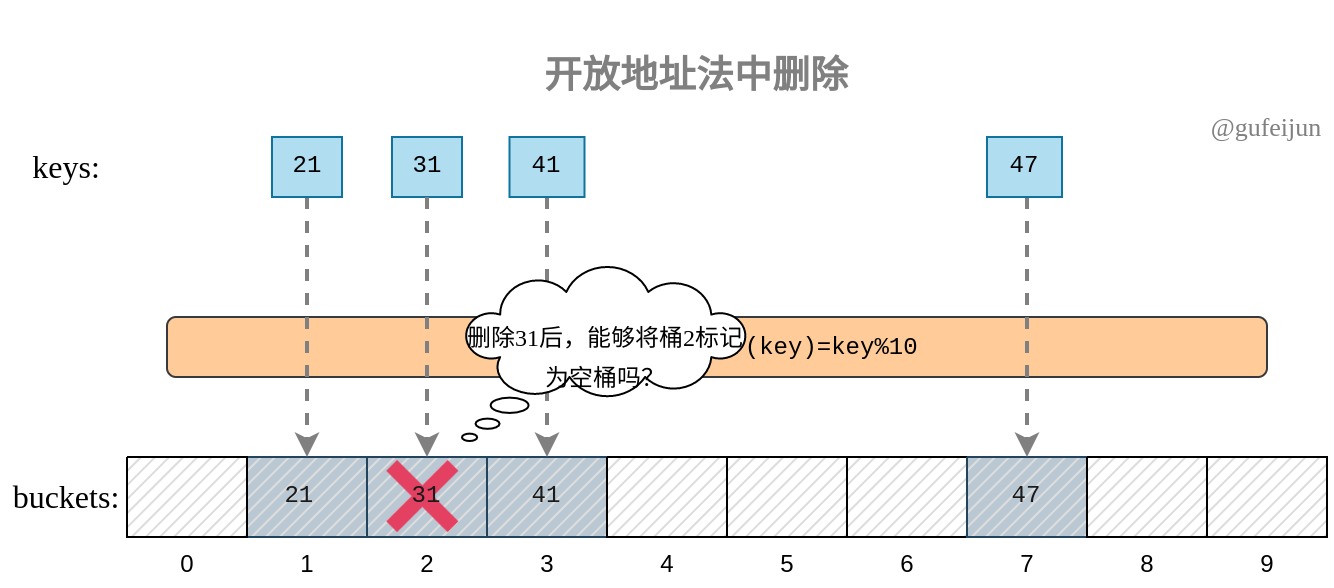
我们的解决方案:一个桶根据是否存储键值对分为空(E)状态以及占用(O)状态,除此之外我们引入第三种删除(D)状态,通过Del删除操作的桶将处于此状态。
当执行查找或者删除操作时,我们将D状态桶以O状态处理,不会在D桶就停止向后迭代查询的过程;但当执行插入操作时,可以将此桶当做E状态处理,也即可以向此桶插入数据。
数据结构以及宏定义:
|
|
提供一个通用的access方法,这个方法将被Set、Get、Del方法使用:
|
|
前面提到,对map的操作,除了要查看哈希指向的桶外,还要因为同义词问题查看后续的一些桶。
对于Get查找以及Del删除这两个查询操作,我们的线性迭代终止于碰到存储了对应key的目标桶或者碰到了空桶,前者代表map中保存了此key,后者表示未保存该key。
对于Set方法,它有两种可能:①map中键已存在,我们将对应桶的value更新。②map中键不存在,我们找到一个空桶或者处于Delete状态的桶进行插入即可。
access方法就是把上述各情况下终止迭代的桶返回,我们再判断桶的state成员即状态,就可以知道该做哪些操作。
Set、Del以及Get方法:
|
|
上面grow方法用于在负载因子过大情况下进行扩容,我们扩容采取桶倍增的方式:
|
|
整体比较简单,理清楚增删改查的过程即可。
拉链法
对于拉链法实现,我们让预先分配内存的桶作为链表的头结点,同义词存在同一个桶后链表中。
欲查询键值对,只需要先通过hash定位到目标桶,然后遍历桶后的所有链表节点即可。欲插入键值对,还需要考虑已经存在键,需要覆盖value的情况。
数据结构定义:
|
|
基础操作方法:
|
|
逻辑方面比开放地址法更简单。如果负载因子过大,则会让每个桶后的链表过长,因此区分同义词还是需要遍历链表,从而使效率变低。甚至在极端情况,所有key都是同义词,查找时间效率最差为O(n)。
我们这里采取的负载因子上限为1,也就说如果哈希均匀的情况下,每个桶后链表仅存储一个节点,查询的时间开销为O(1)。
我们所写的均为最简实现,但已经把拉链法最核心的思想展现,其他的只是些优化技巧,比如哈希的取模操作转化为位运算、预先分配溢出桶、一个桶存取多个键值对减少节点数以优化内存占用以及gc等,这些我们会在go语言的map源码剖析中详解。
总结
从最基本原理角度出发,抛开各种优化,其实实现一个基本能用的hash表也仅仅只需要100行左右代码。
下一节将以红黑树实现map映射结构,同样是以抓住核心本质且最简单的方式实现,帮助你尽快地打破map的神秘感,有个最直观的认识。我相信理解核心思想后,再去阅读那些实现更为复杂的源码,会更为得心应手。
系列目录
- 01、一个系列彻底搞懂map(一):hash表
- 02、一个系列彻底搞懂map(二):红黑树实现
- 03、一个系列彻底搞懂map(三):go语言map剖析
- 04、一个系列彻底搞懂map(终):并发安全map
- 原文作者:辜飞俊
- 原文链接:https://gufeijun.com/post/map/1/
- 版权声明:本作品采用知识共享署名-非商业性使用-禁止演绎 4.0 国际许可协议进行许可,非商业转载请注明出处(作者,原文链接),商业转载请联系作者获得授权。

